
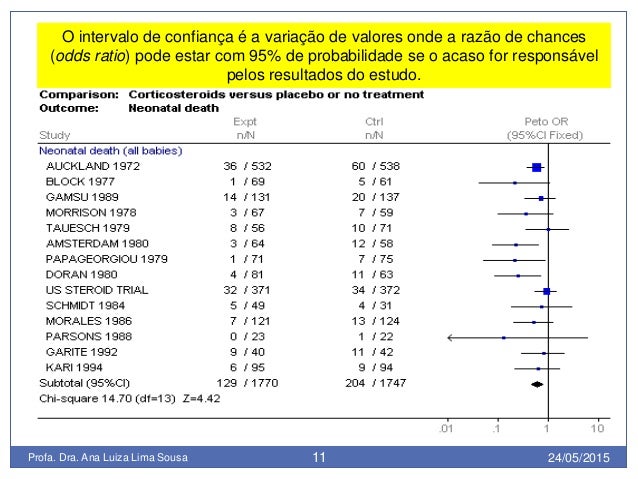
greggii plantations.Ĭuando se desconocen las dimensiones del diámetro normal (dn) de los árboles para calcular el volumen, la relación funcional entre dn y diámetro de tocón (dt) es muy útil. This equation and the ratio factor are reliable tools for estimating dn, and may be applied as the basis for estimating volume, biomass or carbon in P. The average ratio factor between dt and dn was 0.7879. The selected equation included stump height (ht ) and explained 94.86 % of the observed variance, without violating the assumptions of normality of the data, residual homoscedasticity and the autocorrelation of errors.
Predictability was determined with the bias (E), Aggregate Deviation (DA ) and DA percentage (DA %), in addition to the graphical behavior of the predicted values against the observed ones. ), the Root Mean Square Error (REMC), the Akaike (AIC) and Bayesian (BIC) information criteria, the graphical analysis of the residuals and the normality test. With the data from 621 trees, four models were fitted to estimate the dn-dt relation to the PROC MODEL SAS 9.1 statistical package and the gmm procedure.The best model was selected by the fitted Coefficient of Determination (R2 aj. The aim of this study was to generate equations and dn-dt ratio factors for Pinus greggii plantations in the state of Hidalgo, Mexico. When normal diameter (dn) of trees for volume calculations are unknown, the functional relationship between dn and stump diameter (dt ) is very useful. KEYWORDS: contextuality, cyclic systems, double-detection, inconsistent connectedness, psychophysics. Nevertheless our results once again indicate that when inconsistent connectedness is taken into account, the system exhibits no contextuality. Here, we present the results of a psychophysical double-detection experiment that do not form a cyclic system: their analysis requires that we use a recent modification of CbD, one that makes the class of noncontextual systems more restricted. Until recently, however, experimental analysis of contextuality was confined to so-called cyclic systems of binary random variables. When applied to a large body of published behavioral experiments, the CbD computations reveal no quantum contextuality: all context-dependence in these experiments is described by inconsistent connectedness alone. When applied to quantum physical experiments that exhibit inconsistent connectedness (due to context-dependent errors and/or signaling), the CbD computations reveal quantum contextuality in spite of this. The Contextuality-by-Default (CbD) theory separates contextuality from inconsistent connectedness.
The results of behavioral experiments typically exhibit inconsistent connectedness, i.e., they violate the condition known as "no-signaling," "no-disturbance," or "marginal selectivity." This prevents one from evaluating these experiments in terms of quantum contextuality if the latter understood traditionally (as, e.g., in the Kochen-Specker theorem or Bell-type inequalities).


 0 kommentar(er)
0 kommentar(er)
